
I was able to acquire a data set of 1248 barcode sequences, all of them Lepidoptera (butterflies and moths) from Australia. Each entry gives the name of the specimen (if known), the location it was collected, and a 659 base (i.e. ACTG) barcode.
>NSWBB765-08|07-NSWBB-0765|Acantholipes juba AACATTATATTTTATTTTCGGAATTTGGGCAGGTATAGTAGGAACCTCATTAAGATTATTAATTCGAGCTGAACTAGGAA ACCCCGGATCTTTAATTGGGGATGATCAAATTTATAATACAATTGTTACAGCACATGCCTTCATTATAATTTTCTTTATA GTTATACCAATTATAATTGGAGGATTTGGAAATTGATTAGTACCATTAATATTAGGAGCTCCAGATATAGCCTTCCCTCG TATAAATAATATAAGTTTTTGACTTCTCCCCCCATCATTAACATTATTAATTTCCAGTAGAATTGTAGAAAATGGAGCAG GAACTGGATGAACTGTTTACCCCCCACTTTCATCTAATATCGCCCATAGAGGAAGATCAGTTGATTTAGCTATTTTTTCC CTTCATTTAGCAGGAATCTCTTCAATTTTAGGAGCAATTAATTTTATTACGACAATCATTAATATACGATTAAACAATTT AATATTTGATCAAATACCTCTATTTGTTTGAGCTGTAGGAATTACCGCTTTCCTTTTACTACTTTCATTGCCCGTATTAG CAGGAGCTATTACCATACTTCTCACTGATCGAAACCTTAATACATCATTCTTCGATCCAGCAGGAGGAGGAGATCCTATT TTATATCAACATTTATTT-
The first two fields are identifiers, the Acantholipes juba is the collector's guess at the identity of the specimen, and the long field is the DNA barcode. (I have put in line breaks every 80 characters; in the actual file the barcode is all on one line.) By playing with this data, I hoped to answer a few questions.
I started by parsing the data (using a simple Python script) and printing some aggregate statistics:
Number of genomes: 1248 (801 distinct) Multi-named genomes: 0 Genome lengths: min=659, max=659 Character counts: -:1531 A:249466 C:126358 G:120017 N:1505 T:323555
As I said, there are 1248 genome sequences, of which 801 are distinct (that is, 447 are duplicates of some other sequence). Of those 447 pairs of duplicates, none had different identifying names assigned by the collector, so that's a good sign. Every sequence consists of exactly 659 bases. The sequences consist mostly of the familiar ACTG (with significantly more T and A than C or G) but about 0.2% of the total consisted of either "N" or "-". These represent places where it was not possible to get a good read of the actual base.
Now I want to deal with sequences that are similar but not identical. There are two standard ways to measure the difference between two sequences of characters. The first, Hamming distance, just compares the first character of one to the first of the other, etc. and sums the number of places where they mismatch. This might be good enough in a case like ours, where every string has the same length. But I noticed that many strings end in "N" or "-", indicating that they might be truncated, and that the truncation might appear earlier in the string. Consider two strings that are identical, except that one is missing the first character and has a "-" appended at the end. These two would have a high Hamming distance, because the corresponding characters don't match (except by accident). But the Levenshtein distance, which considers insertions and deletions as well as substitutions, would give these two strings a distance of just 1: 1 point off for the deletion of the first character, then 0 distance for all the characters that are the same, then another 0 for matching the "-" against any character. There is a well-known dynamic programming algorithm for Levenshtein distance. I coded this into my script in a few lines, and started it going. But I measured that my naive implementation was taking 0.8 seconds per comparison, and thus would need around a week to compute all the distances between pairs of sequences. So I stopped that job and looked for something more efficient. I easily found a Java implementation by Chas Emerick that did what I wanted. Since it only computes the distance, and does not give the full derivation of the difference between the two sequences, it needs only O(n) storage instead of O(n2). I modified it to match "N" and "-" for free, and to return immediately as soon as the difference reaches 4% of the total number of characters. You can see the resulting Java file and the output it produces (see note on Java verbosity). I then went on to analyze the distance data, creating some histograms:
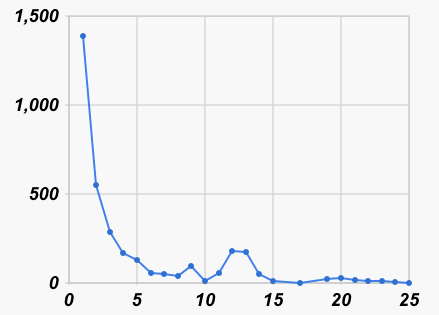
Nearest neighbor counts: 0:774 1:177 2:67 3:16 4:10 5:4 6:1 7:4 9:1 10:2 11:2 12:1 13:2 17:4 25:2 >25:181 Number of neighbors at each distance: 0:5060 1:2774 2:1096 3:570 4:340 5:258 6:112 7:100 8:76 9:194 10:24 11:110 12:356 13:350 14:98 15:20 17:4 19:44 20:52 21:30 22:20 23:20 24:12 25:2
These are easier to visualize with pictures (leaving off the counts for distance 0):
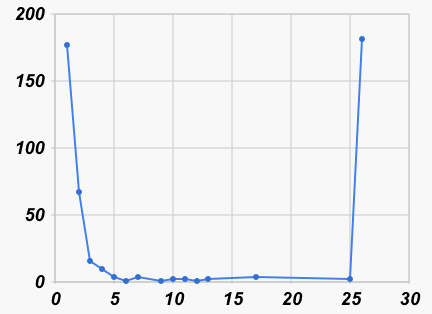 | 
|
| Number of nearest neighbors at each distance | Number of neighbors at each distance |
|---|---|
| (all at distance > 25 shown at 26) | (not counting distance > 25) |
We can see in the graph on the left that most barcodes have a nearest neighbor that is no more than an edit distance of 4 away (it turns out to be 84%). If we look (graph on the right) at all pairs that are within 4% of each other, we see again that many are within a distance of 4, but then there is a small hump at a distance of 12 or 13 (which is 2% of 659), and then very few others at larger distances. So this preliminary analysis is a hint that the species boundary, if it exists at all, might be in the 1% to 2% range.
I decided to start by considering both possibilities at once. That is, I would define a clustering algorithm that takes two parameters, d, the threshold distance to the closest member of the cluster, and dc, the threshold difference to every member (or equivalently, to the farthest member) of the cluster. We call this distance between farthest members of a cluster the diameter of the cluster.
Here is a table of the number of clusters that result for values of d from 0.9% to 2.1% (along the vertical axis) and for dc between 1.7% and 2.4%, as well as 100% (along the horizontal axis). A dc value of 100% means that we are only considering d (and opposite ends of chains in a cluster can be any distance apart).
100% 2.4% 2.3% 2.1% 2.0% 1.8% 1.7%
0.9% ( 6) 390 390 390 390 390 390 390
1.1% ( 7) 386 386 386 386 386 386 386
1.2% ( 8) 384 384 384 384 384 384 384
1.4% ( 9) 383 383 383 383 383 383 383
1.5% (10) 381 381 381 381 381 381 382
1.7% (11) 378 378 378 380 381 381 382
1.8% (12) 377 377 377 379 381 381 382
2.0% (13) 375 375 375 377 381 381 382
2.1% (14) 375 375 375 377 381 381 382
It looks like the median value is about 382, and that the high (390) and low (375) values are within 2% either way of the median. That tells us the variation in the number of clusters, but what about the composition of each cluster? How many of them are variable? We'll consider a cluster half changed if exactly one element is added or subtracted, and fully changed if there are two or more additions or subtractions. Then we consider the list of clusters formed with d=1.7% and dc=2.1%, and get the following table of percent of changes according to this half plus full metric:
100% 2.4% 2.3% 2.1% 2.0% 1.8% 1.7%
0.9% ( 6) 1.7% 1.7% 1.7% 1.7% 1.7% 1.7% 1.7%
1.1% ( 7) 1.2% 1.2% 1.2% 1.2% 1.2% 1.2% 1.2%
1.2% ( 8) 1.0% 1.0% 1.0% 1.0% 1.0% 1.0% 1.0%
1.4% ( 9) 0.9% 0.9% 0.9% 0.9% 0.9% 0.9% 0.9%
1.5% (10) 0.7% 0.7% 0.7% 0.7% 0.7% 0.7% 0.9%
1.7% (11) 0.8% 0.8% 0.8% 0.0% 0.7% 0.7% 1.0%
1.8% (12) 1.2% 1.2% 1.2% 0.4% 0.7% 0.7% 1.0%
2.0% (13) 2.0% 2.0% 2.0% 1.2% 1.4% 0.7% 1.0%
2.1% (14) 2.0% 2.0% 2.0% 1.2% 1.4% 0.7% 1.0%
It looks like the percentage change in clusters is similar to the percentage change in number of clusters. In other words (roughly speaking), as we put tighter bounds on d and dc the main changes are in splitting up a few clusters into finer grained ones; beyond that there is very little additional change where elements change clusters.
Note that if we only consider the d parameter (that is, if we start with some element and then spread out from there, forming a cluster of all elements that can be reached by individual steps of length d or less) then the results will be deterministic--they will be the same every time, regardless of the order in which we consider elements. This is not true of the dc parameter. If we try to keep every element of a cluster with distance dc of each other than we may get different results if we start with different elements. To see if this has a major effect, I modified the clustering algorithm to consider elements in random order, and replicated the tables above. There was almost no difference. (On a minority of the runs, one of the "381" and one of the "383" entries changed to "382". No other changes were observed.)
Now let's look at the margins between clusters: how far are the elements of a cluster to elements of another cluster? For each individual, we ask is it within some multiple of the diameter of its cluster to another cluster? We will answer the question for multiples of 1.2, 1.33, and 1.5. In other words, for 1.2 we are asking how many individuals that we have assigned to a cluster c are also within a distance of 1.2 times the diameter of c to some other individual that is not in the cluster. Here are the results, again for various values of d and dc:
Percent of individuals within 1.20*diameter of another cluster.
100% 2.4% 2.3% 2.1% 2.0% 1.8% 1.7%
0.9% ( 6) 0.0% 0.0% 0.0% 0.0% 0.0% 0.0% 0.0%
1.1% ( 7) 0.0% 0.0% 0.0% 0.0% 0.0% 0.0% 0.0%
1.2% ( 8) 0.0% 0.0% 0.0% 0.0% 0.0% 0.0% 0.0%
1.4% ( 9) 0.0% 0.0% 0.0% 0.0% 0.0% 0.0% 0.0%
1.5% (10) 0.1% 0.1% 0.1% 0.1% 0.1% 0.1% 0.1%
1.7% (11) 0.0% 0.0% 0.0% 3.1% 20.9% 33.4% 1.0%
1.8% (12) 0.0% 0.0% 0.0% 3.1% 20.9% 33.4% 1.0%
2.0% (13) 0.0% 0.0% 0.0% 3.1% 21.6% 33.4% 1.0%
2.1% (14) 0.0% 0.0% 0.0% 3.1% 21.6% 33.4% 1.0%
Percent of individuals within 1.33*diameter of another cluster.
100% 2.4% 2.3% 2.1% 2.0% 1.8% 1.7%
0.9% ( 6) 1.3% 1.3% 1.3% 1.3% 1.3% 1.3% 1.3%
1.1% ( 7) 1.3% 1.3% 1.3% 1.3% 1.3% 1.3% 1.3%
1.2% ( 8) 2.6% 2.6% 2.6% 2.6% 2.6% 2.6% 2.6%
1.4% ( 9) 2.6% 2.6% 2.6% 2.6% 2.6% 2.6% 2.6%
1.5% (10) 2.7% 2.7% 2.7% 2.7% 2.7% 2.7% 2.7%
1.7% (11) 0.0% 0.0% 0.0% 3.1% 20.9% 34.1% 3.6%
1.8% (12) 0.0% 0.0% 0.0% 3.1% 20.9% 34.1% 3.6%
2.0% (13) 0.0% 0.0% 0.0% 3.1% 21.6% 34.1% 3.6%
2.1% (14) 0.0% 0.0% 0.0% 3.1% 21.6% 34.1% 3.6%
Percent of individuals within 1.50*diameter of another cluster.
100% 2.4% 2.3% 2.1% 2.0% 1.8% 1.7%
0.9% ( 6) 26.3% 26.3% 26.3% 26.3% 26.3% 26.3% 26.3%
1.1% ( 7) 25.7% 25.7% 25.7% 25.7% 25.7% 25.7% 25.7%
1.2% ( 8) 51.8% 51.8% 51.8% 51.8% 51.8% 51.8% 51.8%
1.4% ( 9) 51.8% 51.8% 51.8% 51.8% 51.8% 51.8% 51.8%
1.5% (10) 51.8% 51.8% 51.8% 51.8% 51.8% 51.8% 51.8%
1.7% (11) 0.0% 0.0% 0.0% 3.1% 23.5% 57.1% 52.7%
1.8% (12) 0.0% 0.0% 0.0% 3.1% 23.5% 57.1% 52.7%
2.0% (13) 0.0% 0.0% 0.0% 3.1% 24.1% 57.1% 52.7%
2.1% (14) 0.0% 0.0% 0.0% 3.1% 24.1% 57.1% 52.7%
We can see that most of the time the individuals are all or almost all at a distance greater than 1.2 times the diameter. The only exceptions are for the combination d ≥ 1.7% and 2.1% ≤ dc ≤ 1.8%. I have no idea why that combination is bad. At a distance of 1.33 times the diameter the same region is bad, and the rest of the parameter space is up slightly, mostly to between 1.3% and 2.7%. At a distance of 1.5, the results are uniformly bad, with the exception of the lower-left corner of the graph, corresponding to the combination d ≥ 1.7% and dc %ge; 2.3%.
The next step is to compare the clusters generated by the clustering algorithm to the labels recorded by the collectors who gathered the samples. The following table gives the number of clusters that are labeled with more than one name, for various choices of d and dc:
100% 2.4% 2.3% 2.1% 2.0% 1.8% 1.7%
0.9% ( 6) 1 1 1 1 1 1 1
1.1% ( 7) 1 1 1 1 1 1 1
1.2% ( 8) 2 2 2 2 2 2 2
1.4% ( 9) 2 2 2 2 2 2 2
1.5% (10) 2 2 2 2 2 2 2
1.7% (11) 2 2 2 2 2 2 2
1.8% (12) 2 2 2 2 2 2 2
2.0% (13) 3 3 3 3 3 2 2
2.1% (14) 3 3 3 3 3 2 2
This looks good; the algorithm generates very few clusters that the collector thought had different names. If we want to minimize these, we would choose d=0.9% or 1.1%, and would get 390 or 386 clusters. But we know the collectors are not perfect, so that should not be the only criteria.
Now let's look at the labels the other way around. Consider all the specimens with the same label as a cluster, and ask what is the diameter of each cluster according to our metric? There are only 291 such clusters, and most of them have a diameter of 7 or less:
| Number of clusters formed by labels at each diameter |
|---|
There are 17 clusters with a diameter over 2%. We give the diameter, the label, and the number of elements in each such cluster:
diameter 15 for Polyclysta hypogrammata (3 elements) diameter 17 for Compsotropha strophiella (2 elements) diameter >25 for Pyralidae (34 elements) diameter >25 for Agriophara sp. (8 elements) diameter >25 for Tortricidae (54 elements) diameter >25 for Oecophoridae (28 elements) diameter >25 for Musotima (2 elements) diameter >25 for Geometridae (3 elements) diameter >25 for Crambidae (11 elements) diameter >25 for Lepidoptera (31 elements) diameter >25 for Proteuxoa (6 elements) diameter >25 for Plutella xylostella (3 elements) diameter >25 for Edosa (2 elements) diameter >25 for Hellula undalis (12 elements) diameter >25 for Xyloryctinae (4 elements) diameter >25 for Nolinae (4 elements) diameter >25 for Noctuidae (23 elements)
Note that many of these are labeling problems. For example, there are 31 specimens that are gabelled just Lepidoptera (which is the entire Order for "moth or butterfly"); it is no wonder that this cluster has a diameter > 25. Most of the other large-diameter clusters are gabelled with family or subfamily names, not with species.
More generally, "species" is often defined as a "group of organisms capable of interbreeding and producing fertile offspring." That's a start, but it's not a perfect definition. First of all, the majority of organisms do not even reproduce sexually. Birds do it, bees do it, most macroscopic eukaryotes do it, but bacteria and archaea do not, nor do some plants and fungi. Second, what does "capable of" mean? Historically, the Capulets and Montagues did not interbreed (nor the Sharks and Jets), but most observers would say they would be capable. But what is an observer to say about two groups of frogs that disdain each other? How do we know if they are capable of interbreeding? Third, there is the problem of transativity of species membership. Consider the Ensatina salamander. These exist in the mountains surrounding the Central Valley in California. The mountains are laid out in a horseshoe shape, and as you traverse the horseshoe, you notice variations in the salamanders. Each variation can interbreed with its near neighbors, but the ones at the extreme western end cannot interbreed with those at the far eastern end. They can't be all one species, because they don't all interbreed, but then neighboring pairs do interbreed, so there is no clear answer as to where to draw the barriers. Biologists describe this as a ring species which is neither a single species nor a set of multiple discrete species. It seems we have to accept that species is a natural kind term which has clear prototypes -- paradigmatic cases where everyone can agree what is and isn't a species -- but does not have crisp boundaries.
120325 out13.Z 120357 out9.Z 120361 out18.Z 120373 out6.Z 120381 out11.Z 120383 ORIGINAL.Z 120405 out14.Z 120407 out1.Z 120415 out2.Z 120419 out16.Z 120423 out15.Z 120427 out5.Z 120445 out12.Z 120447 out0.Z 120449 out7.Z 120459 out4.Z 120463 out19.Z 120473 out17.Z 120483 out8.Z 120495 out10.Z 120543 out3.ZIn other words, of the twenty trial files, 15 resulted in more information that the original, and 5 resulted in less. I repeated the experiment with 100 output files; this time 91 resulted in more information and 9 in less. I believe this answers the information challenge.
tokens = file("barcodingdata.txt").read().split()
genomes = [t for t in tokens if len(t) > 500]
and all I have to remember is two things that I use every day: that
file objects have a read method and strings have a
split method.
In Java I have to remember or look up eight things: (1) the name of the class to read files, (2) the name of the class to buffer the reader, (3) the fact that I need both classes, (4) the class to tokenize strings, (5,6) the two methods that StringTokenizer uses to enumerate its elements (different from enumerating the elements of a list, vector, or any other class), and finally (7,8) the two classes of exceptions that can be thrown during the process of opening and reading files. That adds up to 15 lines:
public static void main(String[] args) throws java.io.FileNotFoundException, java.io.IOException {
String[] genomes = new String[1280];
BufferedReader reader = new BufferedReader(new FileReader("barcodingdata.txt"));
int N = 0;
String line;
while ((line = reader.readLine()) != null) {
StringTokenizer st = new StringTokenizer(line);
while (st.hasMoreTokens()) {
String t = st.nextToken();
if (t.length() > 500) {
genomes[N] = t;
N++;
}
}
}